AI/주워들은 것들
Fisher Discriminant Analysis(선형판별분석)
아인샴
2024. 3. 23. 01:51
FDA 혹은, Linear Discriminant Analysis(LDA)라고 불린다. Fisher에 의해 제안되었다.
- 데이터들을 하나의 직선(1차원 공간)에 projection시킨 후 그 projection된 data들이 잘 구분이 되는가를 판단하는 방법이다.

- 데이터가 잘 구분되어있다는 의미는 위 그림 중, 왼쪽 보단 오른쪽 처럼 구분돼야 한다고 했다.
- 이 특성을 보자면, 데이터들이 모여있고, 중심부가 서로 멀수록 데이터의 구분이 잘 된 것이라고 한다.
- 즉, projection 후의 두 데이터 중심(평균)이 서로 멀수록(거리), 그 분산이 작을수록(응집) 구분이 잘 되었다고 얘기할 수 있다. 이렇게 잘 분류되게끔 하는 하나의 vector w를 구하는 것이 LDA이다.
w에 projection 된 x들의 평균과 표준 편차를 구하기도 한다. (자세한건 출처1)
- data가 잘 분류되 기 위해서 전체 데이터 분산은 大, 평균은 멀리, 각 class분산은 小, 해야 한다.

전체가 검은선, 빨강과 파랑이 각 클래스다. (각 평균u1 u2가 있다.)
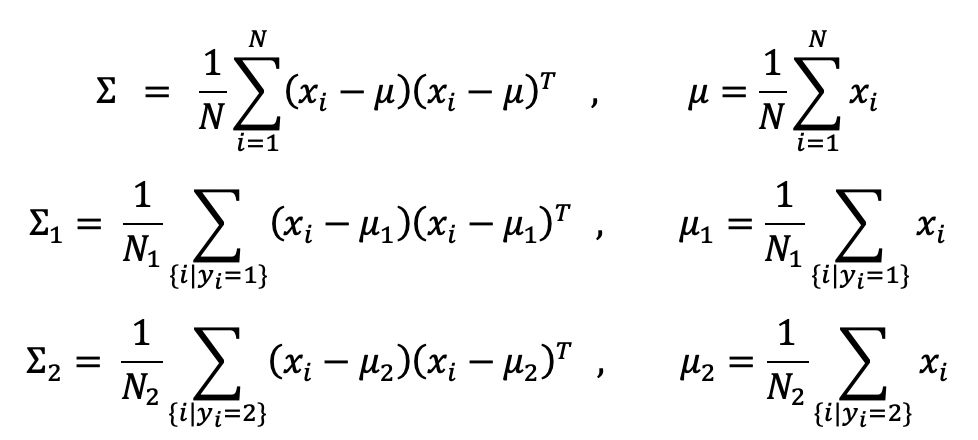
- 다음 조건들을 만족(데이터 분산大, 평균멀리, class분산小)하는 objective fucntion가 아래와 같다고 한다.

분자(데이터부산), 분모(각 클래스 분산); 이 L(w)의 최대값을 갖게하는 w가 optimal solution 이다. - 단점 : 데이터 수가 차원보다 적을 경우 분제가 생긴다고 한다.
- class내부에서 variance가 0이 되는 상황도 생기고 그 방향이 null space가 된다고 한다. 그래서 결과가 많이 달라지고 이를 과적합현상이라고 하는데, Regularization 을 통해 심각한 문제를 덜 심각하게 만드는 것으로 보인다.
- 그 이상은 출처1
- DA에 관련도가 높은 알고리즘같아 관련 수식을 자세히 이해하고 싶지만 시간이 부족해서 여기까지 봐야 할 것 같다. 나중에 더 본다면
- https://minicokr.com/8
- 를 더 보고자 한다.