[LUCIR] CVPR'2019

아인샴 2024. 6. 1. 18:31

Learning a unified classifier incrementally via rebalancing

리딩 이유 : AAnet의 [16]으로 읽었던 CIA 논문에서 2번이상 언급되었음.

리딩 목적 : 현존하는 CIL method 로 무엇이 어떻게 활용된 것인지 확인하고자 한다. 그래서 Abstract만 빠르게 흝는다..!

그림1. multi-class incremental 학습에서의 old/new class 불균형으로 야기된 adverse effect들. 그리고 어떻게 해결할 지를 보이고 있다.

Abstract

전통적인 DNN은 사전준비된 대규모 데이터셋에 의존해 오프라인 훈련한다. 들어오는 데이터흐름을 포함한 온라인 서비스같은 real-world application에선 한계가 있다.
incremental training에서 새로운 데이터에 모델을 적용하는 것은 catastrophic forgetting현상이 발생하는데, 우린 이 원인을 이전 데이터와 새로운 데이터간의 불균형이라 꼽았다.
그래서 old class와 new class를 모두 균일하게 취급하는 unified classifier를 새로운 프레임워크로 개발한다.
구체적으로 데이터불균형의 adverse effects를 완화시키기 위해 cosine 정규화, less-forget constraint, class간 separation의 요소를 통합했다.
실험결과 해당 방법은 우수했고 CIFAR100과 ImageNet에서 10phase간 classifiaction error를 6%/13%씩 감소시켰다.

1. Introduction

Incremental learning은 model 로 하여금 whole dataset을 학습하는 대신 new data를 continually update하는 방식의 학습 패러다임이다. 그러나 catasstrophic forgetting 이슈에 직면해있고, new data로 모델을 fine tuning하면 previous data의 성능이 현저하게 떨어진다.
두 가지 노력이 있었다.
1. original model의 significant parameter를 식별하고 보존하기
2. knowledge distillation을 통해 original model 의 지식 보존
catastrophic forgetting은 완화해도 전체성능을 여전히 joint training에 비해 상당히 낮았다. 본 연구에선 이보다 효과적인 방법탐색을 목표로 하며 unified classifier가 different stage에서 831개 클래스를 학습하는 걸 목표로 한다.
모델이 각 task를 separage group of classes전용으로 하여 서로 다른 작업을 처리하도록 훈련하는 conventional multi-task setting에 비교하여, multi-class setting은 보다 현실적이고 어렵다. 핵심과제는 이전 stage의 old class와 현재 stage의 new class 사이의 imbalance이다.
그래서 그림1과 같이 class별 가중치에 여러가지 부작용을 초래한다.
1. imbalanced magnitude : 새로운 클래스의 가중치 벡터가 이전클래스의 것보다 현저히 높음
2. deviation(편차) : previous knowledge; 이전 클래스의 특징과 가중치 벡터간 관계가 잘 보존되지 않음
3. ambiguities : 새로운 클래스의 가중치 벡터는 이전클래스의 가중치벡터에 가까워지는데, 이것이 종종 모호성을 초래할 수 있다.
이런 문제에 대해 incremental setting에서 unified calssifier를 학습할 프레임워크를 제안한다. 불균형을 완화하기 위해,
1. cosine 정규화 : 이전 클래스와 새로운 클래스를 모함한 모든 클래스에 걸쳐 균형잡힌 크기를 적용
2. less-forget constraint : 이전클래스의 기하학적 구성을 보존하는 것이 목표
3. inter-class separation : 이전클래스와 새로운 클래스를 분리하기 위해 large margin을 유도함.

이 논문은 2.Related Work는 간략하게 보더라도, 3 Our aaproach와 3.1인 background를 위주로 봐야할 것 같다.

2. Related Work

2.1 Incremental Learning

existing works는 주로 2가지가 되었는데, 하나는 paramter-based 과 distillation-based 이다.
Parameter-based : EWC, SI, MAS와 같은 category의 방법론은 original모델에서의 중요한 파라미터를 추정하고 이러한 매개변수를 변경하려할 때 너 많은 패널티를 추가하려고 한다. 방법들의 차이점은 파라미터의 중요도를 계산하는 방법에 있다. 그러나 모든 파라미터를 계산할만할 reasonable한 metric을 설계하는 것이 어렵다.
Distillation-based : original model에서 지식보존을 목적으로 modified cross-entropy loss를 사용하는 LwF(Learning without Forgetting)가 incremental learning에서 도입된다.
- Aljundi et al : different tasks에 대해 multiple network를 training하여 각 test sample중에서 autoencoder로 하여금 선택하게 한다.
- Rannen et al : autoencoder를 통해 old task의 crucial feature를 보존한다.
- Hou et al[Lifelong learning via.../ECCV'18]: new tasks에 적응을 쉽게하기 위해 knowledge distillation 사용
위에서 언급한 작업들은 모두 multi-task setting을 따른다. 즉, trained model은 다수의 classifier를 장착하고, 각각 개별작업으로부터의 데이터에 대해서만 평가된다.
multi-class setting에서 unified classifier로 학습하려는 목표도 있었다.
- Jung et al[19] : domain expantion을 고려하여, unchanged decision boundaries와 feature proximity라는 두가지 속성에 의존하는 해결책을 제안
- iCaRL : 지식 증류와 reprentation learning을 몇가지 구성요소와 결합했다. 예를 들어 nearest-mean-of-exemplars classification과 prioritized exemplar seletcion 같은 구성요소가 있다.
- Castro et al : reserved(제한된) old samples에 대해 정교한 data augmentation의 도움을 받아 성능향상
Discussion
- 우리연구는 distillation-based 에 가깝고 불균형의 부작용을 면밀하게 분석했다. 이전 incremental learning 연구에선 dynamic network structure를 채택하거나 생성모델로 old class sample을 생성하곤했는데 이러한 작업들은 제안한 방법과는 독립적이므로 우리프레임워크에 추가해서 개선을 이룰 수 있을 것이다.

2.2. Tackling Imbalance

크게 data resampling과 cost-sensitive learning으로 나눌 수 있다. 전자는 resampling을 통해 서로다른 클래스들의 training sample balance를 조정하는 것이 목표인 반면, 후자는 loss 조정에 집중한다. 이 작업에서는 sampling 비율이나 loss weights를 조정하는 대신 다양한 측면에서의 incremental learning의 imbalence를 다룬다.
inter-class separation에서 bounndary에 추점을 맞춰 클래스간 불균형에 덜 민감한 margin ranking loss를 도입했다. 해당 연구 중 [9]와 가장 관련이 있다.
Dong et al[9] : 불균형한 데이터가 주어지면 cross-entropy loss 학습 bias를 수정하기 위한 class rectification loss를 제안한다. 우리의 margin ranking loss는 , [9]와 다른 점은 mining of the positives and hard negatives하여 incremental training에서 더 효율적이고 전문화 되어있는 점이다.
특히 negative selection에 대한 class similarity를 정의하기 위해, pretrained model에 의존하지 않는다.

3. Our Approach

그림 2. multi-class incremental learning에 대한 우리의 접근법이다. cosine normalization 때문에 특징과 class embeddings가 기하학적으로 고차원 구에 존재한다. incremental 과정에는 세가지 유형의 loss가 포함된다. 크로스-엔트로피 손실 $L_{ce}$ 말고도 $L_{dis}^{G}$는 features(less-forget constraint)에 대해 연산된 novel distillation loss이며, $L_{mr}$은 $\mathcal{C}_o$ 와 $\mathcal{C}_n$ 분리하기 위한 variant of margin ranking loss(inter-class separation) 다.

포커스는 multi-class incremental classification 문제다. 공식적으로 olda dataset $\mathcal{X}_{\mathrm{o}}$으로 학습된 모델이 있을때 우리는 unified classifier로 하여금 new dataset $\mathcal{X}=\mathcal{X}_{\mathrm{n}} \cup \mathcal{X}_{\mathrm{o}}^{\prime} . \mathcal{X}_{\mathrm{n}}$ 를 기반으로 오래된 클래스 $\mathcal{C}_o$와 새로운 클래스 $\mathcal{C}_n$을 학습하는 것을 목표로 한다.

$\mathcal{C}_o$/ $\mathcal{C}_n$	old class / new class	$\mathcal{X}_{\mathrm{o}}/ \mathcal{X}_{\mathrm{n}}$	old dataset / new dataset
$L_{dis}^{G}$	features(less-forget constraint)에 대해 연산된 novel distillation loss	$L_{mr}$	$\mathcal{C}_o$ 와 $\mathcal{C}_n$ 를 분리하기 위한 variant of margin ranking loss(inter-class separation)

$\mathcal{X}_{\mathrm{n}}$는 $\mathcal{C}_n$만 다루는 large dataset인 반면 $ \mathcal{X}_{\mathrm{o}}^{\prime} ⊂ \mathcal{X}_{\mathrm{o}}$는 old sample 의 아주 작은 subset만 보존한다.
도전 과제 : catastrophic forgetting없이 어떻게 성능을 끌어올리도록 심각한 imbalanced $\mathcal{X}$와 original model를 다뤄서 모든 클래스의 성능을 향상시키는 것이다. 먼저 learning without forgettign(LwP), iCaRL 을 backgorund로 보고 multi-class incremental learning의 불균형에 대해 깊이 파고들 것이다. 제안할 접근방식은 그림2. 에 나와있다.

3.1 Background

LwF 는 multi-task incremental-learning에 knowledge distillation을 도입한 첫번째 작업이며 우린 이것을 다중클래스 세팅에 맞게 조정했다. 각 training sample 에 대해 손실함수는 두 항의 합이다. $L_{ce}$와 distillation loss $L_{dis}^{F}$다. ( $L_{ce}$는 크로스-엔트로피 loss)

각 클래스에 대한 라벨과 그에 따른 확률이 커질 수록 loss가 작아진다.

old class $\mathcal{C}_o$ 에 대한 현재 예측이 original model 에 의한 soft label과 일치하도록 장려한다. ($\tau$는 scaling함수임)

$\mathcal{C}$	지금까지 관측된 모든 클래스 집합	$y$	one-hot ground-truth label
$p$	softmax로 얻은 y에 대한 class 확률	$L_{dis}^{F}$	현재 모델이 원래모델의 behavior을 모방하도록 하는 distillation loss, 이전의 지식을 보존한다.
$p^{ \ast }$	x로 $\mathcal{C}_o$ 에 대해 original 모델이 생성한 soft model	$\tau_i(v)=\frac{v_i^{\frac{1}{\Omega}}}{ \sum_j v_j^{\frac{1}{\Omega}}}$	rescaling함수로,
${\Omega}$	일반적으로 1보다 큰 수로, small value인 가중치를 증가시키기 위해 우리 실험에선 2로 했다.	$\|\mathcal{C}_o\|$	old classes의 수

그러나 우리 연구와 icaRL 둘 다 적용된 LwF가 test sample을 new classes로 분류하는 경향이 발견되었다.
iCaRL: nearest-mean-of-exemplars;각 클래스 $c_i \in \mathcal{C}$ 에 대해서 보존된 모든 sample의 특징의 평균을 구하여 프로토타입 $\mu_{i}$를 계산한다. 추론과정에서, test sample의 특징을 추출한 뒤, 가장 유사한 프로토타입 클래스의 레이블을 할당하는 것이다. iCaRL은 LwF의 개선을 이뤄냈지만, long sequence를 가진 class의 경우에는 만족스럽지 않았다.
그래서 앞서 3가지 해결전략을 제시했고 이제 그걸 설명하겠다. (코사인정규화, less-forget 제약, 클래스간 분리)

3.2 Cosine Normalization

일반적인 CNN에서 sample x의 예측확률은 다음과 같이 계산한다.

sample x에 대한 확률은 x를 통해 뽑은 feature와 현재클래스(i) 에 대한 가중치를 곱하여 편향을 더한 것이다. j는 모든 가능한 class index로 보인다. 이렇게 모든 클래스가 나올 확률로 나눠서 x가 i class일 확률을 구한다.

$f$	feature extractor	$\theta/ b$	last layer의 class embedding weights와 bias 벡터
$\bar{v} = \frac{v}{ \\| v \\|_2 }$	$l_2$ normalized vector	$\langle {\bar{v}}_1,{\bar{v}}_2 \rangle ={\bar{v}}_1^T{\bar{v}}_2$	두 normalized voector 사이의 cosine 유사도를 측정한다. $\langle {\bar{v}}_1,{\bar{v}}_2 \rangle$의 범위는 [-1,1]로 제한된다.
η	The learnable scalar; softmax 의 peak를 제어하기 위해 도입했다.	$f^{\ast}/ \theta^{\ast}$	original 모델의 feature extractor와 class embeddings

old / new class에 대한 last layer의 weight와 bias를 시각화 했다. 결과는 iCaRL에 의한 CIFAR100의 incremental setting (1phase)에서 나온 것이다.

그림3과 같이 class imbalence로 인해 임베딩의 크기와 $\mathcal{C}_n$에 대한 편향이 $\mathcal{C}_o$의 편향보다 훨씬 높았다. 이로인해 $\mathcal{C}_n$를 선호하는 예측 편향이 발생했고. 우리는 이를 해결하기 위해서 last layer에 코사인 정규화를 도입했다.

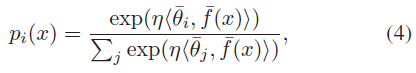
cosine 유사도를 구한뒤 학습가능한 스칼라를 곱한 후 l2 norm을 적용하여 class i에 해당하는 확률을 구했다.

이제 코사인 정규화에 기반한 incremental learning의 sectioin 3.1을 다시 살펴보면, sample x의 경우 classification loss $L_{ce}$가 different way로 계산된 점을 제외하고는 Eq(1)과 같다는 것을 알 수 있다. (?)
distillation loss의 경우 original model과 현재의 η가 다르기 때문에 softmax이후의 확률대신 soft max이전의 score를 모방하는 것이 합리적이었다. 코사인 정규화 때문에 softmax이전의 점수는 모두 [-1,1] 범위에 해당하므로 비교가 가능(comparable)하다. distillation loss는 다음과 같은 공식으로 갱신된다.

cosine 유사도, l2 norm에 이어 original model의 class embedding과 특징추출값의 차이를 loss화 시켜서 기존모델과 유사하도록 유도했다.

기하학적으로 normalized featrue and class embeddings는 고차원 구에 존재한다. $L_{dis}^{C}$ 는 feature과 old class embeddings 사이의 angle에 의해 반영된 기하학적 structrue가, current network에 approximately 하게 보존되도록 유도한다.

3.3 Less-Forget Constraint

catastrohphic forgetting을 완화하고자 $L_{dis}^{G}$라는 새 loss를 도입했다. 이 녀석은 $L_{dis}^{C}$와 비교하여 이전의 지식에 대한 강력한 제약조건(constraints)을 제공한다. $L_{dis}^{C}$는 주로 local geometric struectures( normalized features나 old class embeddings 사이의 angles)를 고려하였는데, 이 제약조건은 그림4처럼 임베딩과 특징이 완전히 회전(rotated entirerely)하는 것을 방지할 수 없었다.

그림4. less-forget constraint. features의 제약조건은 fixed old classes의 임베딩 angles의 제약조건보다 강력하다. (?)

(GPT4)그림4 : angle 제약은 class embedding에 따라 feature가 일정 각도 α를 유지했다. feature 제약에서는 실제 feature vector의 위치에 집중하여 old class embedding 에 좀 더 tight하게 접근했다. 이 접근법은 본래 위치 보다 features가 얼마나 벗어나는지를 직접적으로 제약하기 때문에 더 강력하다. (이 접근법의 목적은 이전 feature vector의 위치를 제약함으로써 forgetting old classes를 완화하려는 것이다.)
그래서 이전 클래스 임베딩을 수정하고 novel distillation loss를 다음과 같이 수정했다.

$L_{dis}^{G}$ 를 통해 이전에 추출된 특징들과 새로운 특징의 차이가 크지 않도록 cosine 유사도를 구했다.

$ \bar{f}^{\ast}(x) $	original model의 extracted features	$\bar{f}(x)$	current model의 extracted features
$L_{dis}^{G}$	$\bar{f}(x)$의 방향을 $ \bar{f}^{\ast}(x) $ 와 유사하도록 유도함( $ \bar{f}^{\ast}(x) $ ≤2)	${\lambda}_{base}$	각 dataset에 대한 fixed constrant
$\lambda $	일반적으로 $\|\mathcal{C}_o\|$에 대한 $\|\mathcal{C}_n\|$ 의 비율이 커지면 증가한다.

이 설계의 근거는 class embedding의 공간구성이 어느정도 클래스간의 고유한 관계를 반영하기 때문이다. 따라서 previous knowledge를 보존하기 위해 자연스럽게 이 구성을 유지시켰다. fixed old class embedding 에서, features가 $L_{dis}^{G}$에서와 유사하도록 유도하는 것이 합리적이다.
실제로, 각 phase에서 도입되는 $|\mathcal{C}_n|$가 다르기 때문에 (10 vs 100) 보존할 지식의 정도도 다양하다. 그래서 $L_{dis}^{G}$의 가중치 $\lambda$를 설정하여 도입했다.

이 $\lambda$를 통해서 이전 지식을 얼마나 보존할 것인지의 loss를 가중치를 통해 제어한다.

최근 연구[19](Jung et al)에선 one-phase incremental learning으로 취급될 수 있는 domain expansion을 다뤘는데, 여기서도 last layer를 fix하고 original model의 특징을 모방할 것을 제안했다.
그러나 우리의 연구는 3가지 측면에서 다르다.
1. distillation loss $L_{dis}^{G}$는 orientation of feature(특징의 방향)만 고려할 뿐 크기는 고려하지 않는다. (특징이 loss에서 normalized되었기 때문에), 이는 모델이 새로운 class에 fit하는데 더 많은 flexibility를 제공한다.
2. 우리는 distillation loss를 phase에서 weight 하기 위한 adaptive coefficient 를 도입했다.
3. 우리의 실험은 proposed method가 long sequence of classes (e.g 10phases)와 보다 현실적인 dataset Image Net에서 잘 동작하는 것을 보여줬는데 이런 것들은 [19]에선 안 이뤄졌다.

3.4 Inter-Class separation

Another practical challenge for multi-class incremental learning : new classes가 training set을 지배한다는 점에서, old class와 new class를 합친 unified classifier를 형성하는 것은 도전과제다.
old/new class 모호성을 피하기 위해 margin ranking loss를 도입하여 class를 분리시킬 것이다. old class의 보존된 sample들을 잘 활용하여, 각 reserved sample x에 대해 x자체를 anchor로 사용하여 all new classes에서 ground-truth old class를 분리하려 한다.
ground-truth class embedding을 postive로 간주하여, hard negatives를 찾기 위한 online mining method를 제안한다. 따라서 제안된 margin ranking loss는 아래와 같다.

hard negative를 찾기위해 기존 ground-trut class embedding에 대한 상위 K개를 margin loss로써 선정하여 가장 큰 것을 loss로 활용한다. class embeding이 ground truth 와 negtative 후보군의 cosine유사도를 계산해서 차이가 작으면 m이 남아서 loss가 커질 것이고 차이가 크면 m이 작아져서 loss도 작아지는 것으로 보인다. .

m	margin threshold	$\bar{\theta}(x)$	x에 대한 ground-truth class embedding
$\bar{\theta}^k$	x에대한 hard negative로 선택된 top-k 클래스 임베딩 중 하나	$\mathcal{N}$	$\mathcal{X}$로부터 추출한 training batch
$\mathcal{Na}_o$	$\mathcal{N}$에 포함된 reserved old samples	$\lambda$	식(7)의 loss weight

각nchor에 대한 postive와 negative는 sample대신 class embedding을 활용했다는 점에 대해서 주목할 만하며, proposed loss는 data sampling process를 변경하지 않고 training process에서 원활하게 통합될 수 있다.

3.5 Integrated Objective

위에 말한 것처럼 세가지 항으로 구성된 총 loss는 다음과 같다.

training phaase가 끝날 때, 우리는 all observed classes에서 가져온 reserved samples의 집합을 통해 보다 balaneced 한 형태로 모델을 finetuning할 수 있다. 소위 말해 class balence finetuing이 실제로 성능을 적당히 향상시킬 수 있다는 것을 발견했다.